Model electricity and other energy markets.

Electricity Network Modeling
Model electricity transmission and distribution networks.
Power flow
Run AC three phase balanced power flow simulations.
Optimal power flow
Run AC optimal power flow dispatch models.
Unit commitment and economic dispatch
Run nodal and zonal network-constrained unit commitment and economic dispatch optimization models using DC-OPF or transport-based transmission representation.
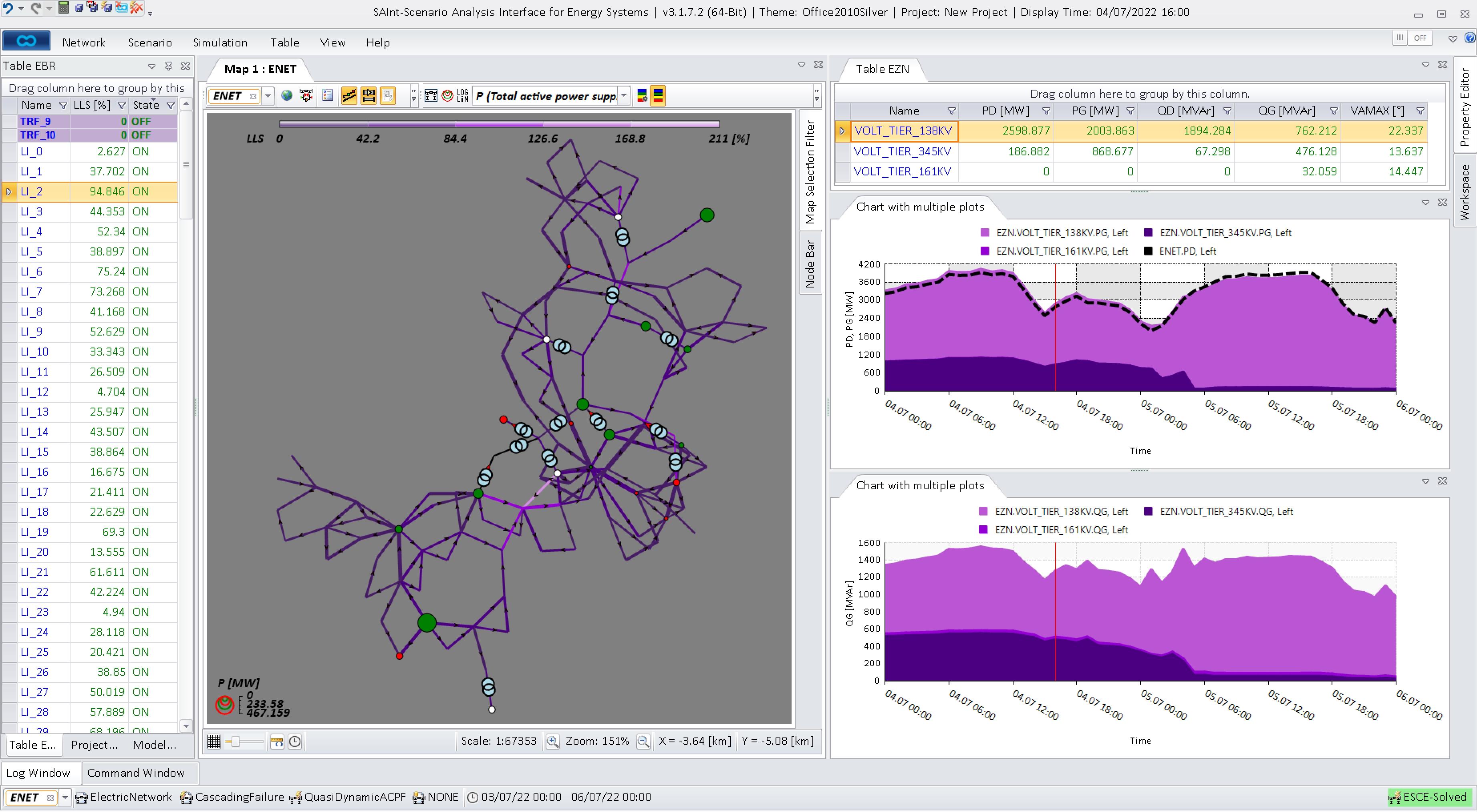
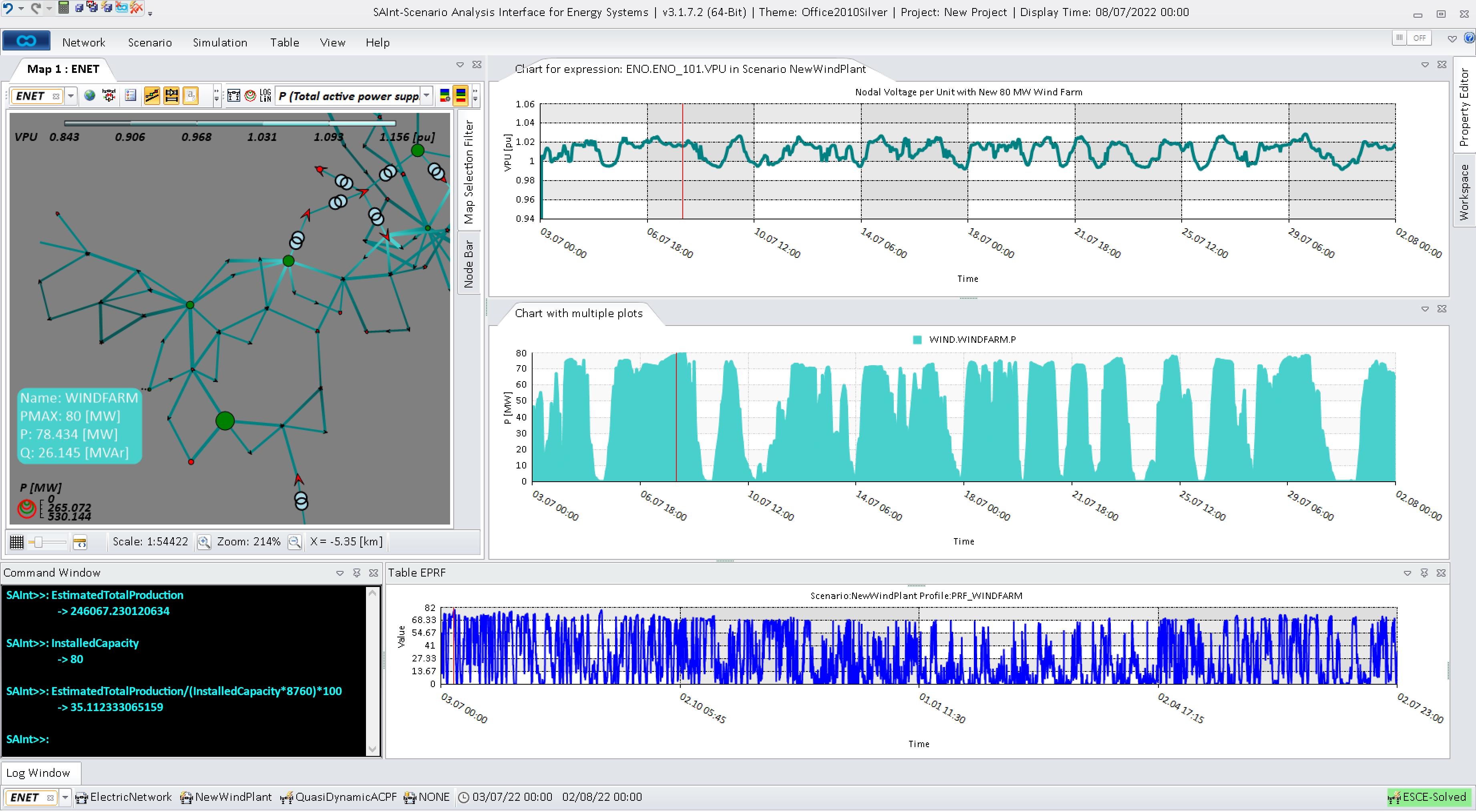
Generation, storage, demand, transmission, and distribution
Model constraints and costs of different power system assets, including generators, lines, transformers, storage devices, and demands.
Probability analyses
Perform reliability studies and risk assessments by evaluating 1,000s of scenarios using SAInt’s flexibility to Run Monte-Carlo simulations.
Model electricity generation profiles of wind and solar plants by leveraging SAInt’s integration with high spatial- and temporal-resolution meteorological datasets.
Other ways SAInt can help you...

Gas Network Modeling
Model gas pipeline transmission and distribution networks.

Coupled Electricity and Gas Network Modeling
Model the synergies and interdependencies between electricity and gas networks.

Thermal Network Modeling
Heating and cooling networks create their own unique challenges

Want the technical flyer?
Check out our flyer on electricity planning to learn more.


